Из комментов в ЛинкендИн: формула удвоения прибыли
Дискуссия вокруг расхожей формулы - увеличьте свои четыре пи на 15% и получите удвоение прибыли - может оказаться неверной в контексте управления продажами интернет-магазина. А какая формула верная? Об этом развернутый коммент...

Смотреть картинку в полный размер
(ц)"Формула такова: Прибыль=лиды*конвертация*средний чек*количество покупок*маржа Если каждый показатель увеличить на 15%, то прибыль удваивается. Математика подтверждает 1,15 умножая пять раз получаешь 2,01..."
--
Конечно же, это обман зрения. Объясню:
== В чем подвох ==
1. Средний чек, по определению, это отношения суммы продаж к количеству чеков. Это - не физическая величина, а расчетная, зависимая переменная.
2. Любой процесс можно разложить на любое количество множителей. Например, если иметь в виду 8 множителей, то повышение каждого на 15% даст вам "прирост в 3 раза". Проблема в том, чтобы это были разные и независимые источники роста, а в вашей формуле это не так (См. п.1).
3. "Без затрат" не бывает. Если вы не тратите свои деньги, значит вы тратите чужие деньги или свое время или чужое время, что все равно есть деньги.
4. Принцип "а давайте мы сначала устраним все потери, и сразу получим эффект" - не масштабируется, он действует только один раз и только для очень плохо организованного бизнес-процесса.
Конструктивное позитивное решение задачи – в следующем посте…
-----------------------------
…Конструктивное позитивное решение задачи.
=== Правильная Модель VPM ==
Вот продажи, разложенные на физические независимые переменные.
Тогда ваши продажи G=Vi*Vm*(P0+P1+P2), а ваша гросс-маржинальная прибыль GM=Vi*Vm*(P0+P1+P2)*M. Прибыль за вычетом затрат =GM-E.
Продолжение в следующем посте….
--------------------------------
…Продолжение.
== Что еще можно посчитать с помощью VPM ==
Прирост продаж/прибыли dG есть разница между G и G0, где G0=Vi*Vm*P0. При этом затраты на поддержание продаж G0 не равны нулю E0>0.
В свою очередь источники прироста продаж делятся на:
На осуществление каждого из них потребуются затраты E(dG). Сопоставив затраты на прирост и результаты прироста продаж E(dG)/dG можно выбрать наиболее эффективный путь прироста, достигнуть его, затем перейти к другим мероприятиям и т.д. При присутствии навыков вариационного исчисления, можно добиться весьма точной величины прироста продаж в зависимости от комбинации усилий и распределения затраты на них (тензор инвестиций E(Vi,Vm,P1,P2)).
---Чисто математическое замечание.---
При этом (важно!) если вы рассчитываете по дифференциалам dG для каждой переменной, расчетная сумма будет ниже реальной, т.е. в реальных продажах добавится еще и синергетический эффект от старших членов бинома. А вот перемножать все переменные вместе с их приростом – с математической точки зрения необоснованно оптимистично. Реальный прирост продаж dG лежит внутри неравенства, причем ближе к нижнему значению:
dVi*Vm*P0+dVm*Vi*P0+Vi*Vm*P1+Vi*Vm*P2<dG<(Vi+dVi)*(Vm+dVm)*(P0+P1+P2)-Vi*Vm*P0.
== mROI ==
Ну тут все просто, если есть данные по предыдущим расчетам, то можно посчитать возврат инвестиций в прирост:
mROI=(dGM-E)/E.
Возврат инвестиций в удержание считается немного по-другому – если интересно, расскажу.
 Структура воды
Структура воды Статьи
Статьи Статьи по теме 'comments'
Статьи по теме 'comments' Из комментов в ЛинкендИн: формула удвоения прибыли
Из комментов в ЛинкендИн: формула удвоения прибыли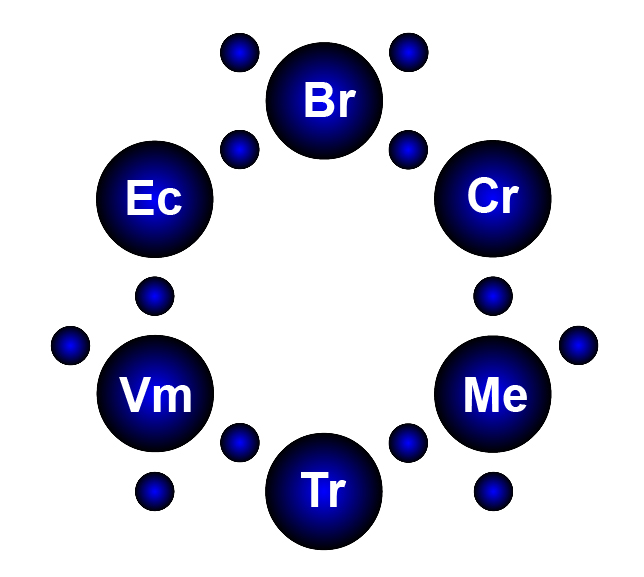
 ВОПРОСЫ-ОТВЕТЫ
ВОПРОСЫ-ОТВЕТЫ СТАТЬИ
СТАТЬИ КОНТАКТЫ
КОНТАКТЫ СБРОС
СБРОС ПОДСКАЗКИ
ПОДСКАЗКИ Клуб СВ
Клуб СВ Карта сайта
Карта сайта